Herkes için Kuantum Teorisi
Kuantum Teorisi, atom ve atomaltı ölçeklerde meydana gelen olayları açıklama yolunda oluşturulmuş kapsamlı bir bilimsel bilgi birikimidir.
Bu birikim, insanlık tarihinde bilimsel ortak aklın ürettiği belki de en önemli, en kapsamlı doğa kavrayışıdır. Biz bu yazıda bu doğa kavrayışının gelişimini tarihsel akışı içerisinde ele alacak, bu teoriyi ilk kez okuyacaklar için ise yine öncesinde yaptığımız gibi sade, anlaşılır olmaya çalışacak, tabi bunu yaparken konuyu asıl bağlamından koparmamaya da gayret edeceğiz.
Bu birikim, insanlık tarihinde bilimsel ortak aklın ürettiği belki de en önemli, en kapsamlı doğa kavrayışıdır. Biz bu yazıda bu doğa kavrayışının gelişimini tarihsel akışı içerisinde ele alacak, bu teoriyi ilk kez okuyacaklar için ise yine öncesinde yaptığımız gibi sade, anlaşılır olmaya çalışacak, tabi bunu yaparken konuyu asıl bağlamından koparmamaya da gayret edeceğiz.
Kuantum teorisini anlatabilmek, anlayabilmek esaslı bir iştir. Ama bunun altından kalkmayı daha önce başarmıştık. (Genel Görelilik)
Bu zorlu yolculukta sizlerle birlikte olmaktan mutlu ve onurluyum. Birbirimize destek olarak bu işi de mutlu sonla bitireceğimize eminim.
En sıradan bir konuyu anlayabilmek için bile bazı kavramları tanımak ve bazı temel bilgilere sahip olmak gerekir. Kaldı ki, konu Kuantum Teorisi olunca, haliyle bu konuda çok daha özenli ve disiplinli olmamız, temeli daha sağlam atmamız gerekiyor.
Bu yazının ilk bölümü temel kavramların tanıtılması ve ışık ve atom fikrinin tarihsel gelişimine ayrılacaktır.
Şimdi biraz ışığın doğası üzerine konuşalım istiyorum. Arada temel kavramları da tanıyacağız.
Işığın davranışı üzerine yapılan çalışmalar çok eskilere dayanır. Yani optiğin temelleri üzerine neredeyse bin yıllık külliyat vardır. Ancak konu ışığın davranışları değil de "doğası" olunca, işler sarpa sarıyordu. Işık neydi? Nasıl yayılırdı? Sorular, sorular...
Işığın doğası üzerine -ve optik- kafa patlatan en önemli isim Isaac Newton idi.
Karanlık bir odaya sızan gün ışığını prizmadan geçirerek onu bileşenlerine ayırmıştır. Beyaz ışığın sanıldığı gibi tek renk olmadığı, aksine birçok farklı renkteki ışığın bir karışımı olduğu anlaşıldı. Çok geçmeden bunun sadece görünen renklerle sınırlı olmadığı anlaşıldı.
Kırmızı ve Mor ışığın "ötesinde" gözle görünmeyen başka ışınların da var olduğu deneysel olarak ortaya konuldu.
Anlaşılan beyaz ışık dediğimiz şey, çok sayıda görünen ve görünmeyen "ışının" bir karışımı idi.
Peki bu ışık nasıl yayılmaktaydı? Bir mermi gibi gibi mi yoksa bir su dalgası gibi mi? Anlaşılması uzun sürmedi. İngiliz Thomas Young ışığı çift yarıktan geçirerek onun bir dalga gibi girişim yaptığını gösterdi.
Ekranda birbirini takip eden aydınlık ve karanlık çizgiler oluşmuştu (Bu deney ileride daha detaylı ele alınacaktır).
Peki nedir bu dalga? Size bir dalganın temel özelliklerini kısaca anlatayım hemen.
İki dalga tepesi ya da çukuru arasındaki mesafeye (bir tam devir) dalgaboyu denir. Bir saniyede üretilen dalga sayısı ise frekanstır. Dalganın tepe yüksekliği (veya çukur derinliği) ise şiddeti, gücü veya genliğidir. Yine çok geçmeden büyük bilim insanı James Clerk Maxwell ışık dalgalarının bir elektrik ve manyetik karakteri olduğunu ortaya koydu.
Yani ışık için "Elektromanyetik Dalga" demek mümkündü. Burada size birkaç cümlede anlattığım şey 150 yıllık çalışmaların ürünüdür. İşte size elektromanyetik dalgaların yani ışığın tayfı ya da başka bir deyişle spektrumu! (siz yelpazesi gibi de düşünebilirsiniz).
Gözünüzün görebildiği aralığın tayf içinde ne kadar küçük bir kesire denk geldiğini fark ettiniz mi? Peki ışığın enerjisinin arttıkça dalga boyunun azaldığını fark ettiniz mi? (Dalgaya dikkat edin)
Enerjisi en yüksek ışınların (dalgaboyu en kısa) gamma, en düşük olanların ise radyo dalgaları (dalgaboyu en uzun) olduğuna dikkat edin.
Dalgaboyu uzadıkça dalganın frekansı azalır. Dolayısıyla radyo dalgaları en düşük frekansa sahip ışınlardır da diyebiliriz. İleride göreceğiz, bir ışın demetinin enerjisi sadece frekansı (dolayısıyla dalgaboyu) ile orantılıdır.
Şimdi atom modellerinin tarihsel gelişimine sırayla ve hızlıca bir göz atalım.
Atom kelimesi, Yunanca a-tomos yani "bölünemez" kelimesinden türemiştir. Ancak zaman Yunan filozoflarını haksız çıkarsa da, ismi aynı kaldı.
Bilimsel anlamda ilk atom modelini John Dalton ortaya attı. Atom yekpare bir küre şeklinde olmalıydı ve yine "bölünemez".
Ancak, atomun aslında yekpare bir parçacık olmadığının ilk bilimsel kanıtları William Crookes'in kendi adını taşıyan tüp ile yaptığı çalışmalarla ortaya kondu. İşte size Crookes tüpü diğer adıyla "Katod ışınları tüpü"
Bu tüp içerisinde parıldayan ve elektriksel manyetik alanlardan etkilenen bir ışın türü keşfedildi. "Katot ışınları". Bu ışınlar üzerine detaylı çalışmalar yapan J.Joseph Thomson bu ışınların aslında negatif yüklü parçacıklar olduğunu oraya koydu.
Bir başkası ise adını çoktan koymuştu bile; George Stoney bu parçacıklara "Elektron" adını verdi. Elektrona "Hoşgeldin" dedikten sonra, geriye içinde elektronun olduğu bir atom modeli resmetmek kalıyordu. Thomson bunu yaptı. Tabi negatif elektron dışında henüz bilinmeyen bir de pozitif yük olmalıydı yoksa atom yüksüz olamazdı. Thomson şöyle bir model önerdi:
Thomson'un "üzümlü kekinin" (modeline öyle deniyor :-) ) ömrü fazla uzun sürmedi. Yeni Zelanda asıllı bir İngiliz çıktı ortaya. Ernst Rutherford, yaptığı altın levha deneyi ile pozitif ve negatif yüklerin atomda homojen dağılmadığını, aksine pozitif yüklerin atomun tam merkezinde küçücük bir hacimde toplandığını gösterdi. Elektronlar ise bu çekirdeğin etrafında dönmekteydiler.
Bu modelin de bazı sıkıntılarının olduğunun anlaşılması uzun sürmedi. Bohr atom modeline geçmeden önce tekrar ışık konusuna dönmeliyiz. Joseph von Frauenhofer. Kendisinden çok kısa bir süre önce Güneş’ten gelen ışığın tayfında karanlık çizgiler keşfedilmişti.
Frauenhofer bu karanlık (siyah) çizgileri detaylı bir şekilde inceledi.Bu nasıl olabilirdi? Birşeyler ışığın tayfındaki belli bölgeleri “soğuruyordu". Bunlara bundan sonra soğurma veya Absorpsiyon spektrumu diyeceğiz.
Frauenhofer bu incelemeleri yaparken Dalton, atom modelini daha yeni oluşturmuştu. Daha elektrondan bile haberleri yoktu.
Bir süre sonra başka yerlerden ayrı ayrı, ama aynı şeyi gösteren keşifler geldi. Anlaşılan ışık ile atomlar arasında bir bağ vardı.
Gustav Kirchoff ve Robert Bunsen ısıtılan elementlerin kendilerine özgü renklerde ışınlar yaydıklarını farkettiler. (Spektral Analiz)
Ancak yine herşey için çok erkendi. Buna bir anlam verecek kuramsal altyapı yoktu. Elektron bile daha yeni keşfedilmişti.
Kirchoff ve Bunsen ne bulmuş bir bakalım. Aşağıda ışığın görünen aralıktaki sürekli spektrumunu (tayfını) görüyoruz.
Burada ise Frauenhofer'in daha önceden keşfettiği karanlık çizgilerin olduğu "Soğurma Spektrumu"nun basit bir modelini görüyoruz.
Bakın burada da Kirchoff ve Bunsen'in keşfettikleri atomlardan yayılan "Emisyon Spektrumu" var. Birşey farkettiniz değil mi?
Emisyon Spektrumundaki renkli çizgilerin Soğurma Spektrumundaki karanlık bölgelere cuk oturduğunu gördünüz mü? Her ne hikmetse, atomlar ışığın belli frekanstaki bölgelerini emiyor yani soğuruyor ve bir şekilde soğurduklari bu ışığı kendiliğinden (veya ısıtıldığında) geri yayınlıyorlardı yani emite (Emisyon) ediyorlardı. İlginç değil mi?
Bakın aşağıda Bunsen alevinde (kendi adıyla anılan) ısıtılan bazı elementlerin özgün ışımalarını görüyorsunuz;
Burada ise yine bazı elementlerin yaydıkları ve görünür bölgeye denk gelen bazı ışımaları görmektesiniz.
Rutherford'un atom modeli bu durum karşısında kilitlenip kalmıştı. İmdada Danimarka'lı bir deha yetişti, Niels Bohr. Ona göre yapılması gereken elektronları enerji seviyeleri birbirinden farklı katmanlara yerleştirmekti.
Bu modelde, elektronlar enerjileri farklı katmanlara yerleşirler. Şayet ışık gelir de bir elektrona "belli büyüklükteki" enerjisini aktarırsa, elektron daha yüksek enerjili üst katmanlara sıçrar. (Işığın spektrumundaki karanlık çizgi enerjiyi veren ışının olduğu yer).
Elektron sıçradığı yüksek enerjili katmanda fazla duramaz, "ben köyümü özledim" der ve geri döner eski katmana. Bu esnada ne mi olur? Aldığı enerjiyi ışık olarak hem de aynı miktarda geri yayınlar (Emisyon Spektrumu).
İkinci Bölüm: Klasik Fiziğin ufkunda toplanmaya başlayan kara bulutlar: Fırtına yaklaşıyor...
19.yy başlarından itibaren (1800'lü yıllar boyunca) fizikçi ve kimyacılar anlamlandıramadıkları bir dolu keşfe imza attılar. Neredeyse her buluşa "ufo gören masum köylü" havasıyla bakıyorlardı desem çok abartmış olmam. Çünkü kuramsal zeminleri zayıftı.
Bunlardan ilkini görmüştük; Frauenhofer, Kirchoff ve Bunsen'in gözlemledikleri garip çizgiler.
Bu bölümde klasik fiziğin kâbusu olan 3 olayı ele alacağız;
a) Fotoelektrik (Fotovoltaik) efekt
b) Radyoaktivite
c) Kara Cisim problemi
Biz bu olayları -ya da keşifleri- bilmeden, Kuantum fikrinin nasıl doğduğunu anlayamayız. Fotoelektrik etki ile başlayalım mı?
Alexandre Edmond Becquerel. Yıl 1839. 19 yaşında. Babasının laboratuvarında çalışırken ilk fotovoltaik düzeneği kuruyor.
İyi de fotovoltaik ne demek? Şu; üzerine ışık düşen bir plakada elektrik akımı oluşur. Bunu açıklayamadı tabi, sadece tarihe not düştü.
Aradan epeyce bir zaman geçtikten sonra 1887'de R.Heinrich Hertz aynı etkiyi bu kez UV ışık altında inceledi. Yine anlam verilemedi.
Yine de Hertz konuyu Annalen der Physik'e (o zamanların en önemli bilimsel yayınlar dergisi) taşıdı: "Bakın millet böyle birşey var duyun"
Madem Hertz'den konuyu açtık, onun elektromanyetik dalgalar üzerine (kısaca EM dalgalar diyeceğiz) çalışmaları olduğunu da söyleyelim.
Kendisi radyo dalgalarını keşfetmiştir (hani şu enerjisi en az, dalgaboyu en uzun olan ışınlar vardı ya, hah işte o :-) )
Derste kendisine "hocam başka tür EM dalgalar var mıdır" sorusuna Hertz, "Hiçbir şey, sanırım.. " demiştir. Ama yanılıyordu...
8 Kasım 1895. Laboratuvarında deli gibi çalışan bir adam: Wilhelm Conrad Röntgen...
Hani şu CROOKES TÜPLERİMİZ vardı ya, (unutmadınız değil mi? :-) ) işte o tüplerle deneyler yaparken tuhaf birşey oldu.
Oldukça girişken bir ışın oluşmuştu; hatta elini bu ışınların önüne koyduğunda Baryum Platino siyanid ekranda el iskeletini gördü.
Wilhelm Röntgen hocamız bu ışınlara "X ışınları" adını verdi. Çünkü ne olduğu hakkında hiçbir fikri yoktu.
Komik bi anekdot gireyim; karısı Anna Bertha bu keşiften yaklaşık iki hafta sonra bu ışınların önüne kendini koyunca ekranda bütün vücut iskeletini görmüş ve korkusundan "ölümümü gördüm" diye çığlık atmıştır. :-)
Antoine Henri Becquerel. Soyadı tanıdık mı geldi? Az önce tanıdığınız Edmond Becquerel'in oğludur kendisi :-)
Becquerel, Röntgen'in X ışınlarını keşfetmesinden 1 yıl sonra bu ışınların doğasını araştırırken bambaşka bir şey bulacağını ne bilsindi?
Bazı tuz bileşiklerini güneş ışığına maruz bırakıp sonra da bunların yaydıkları ışınları fotoğraf filmine alıyordu. Bir gün babasından emanet kalan bir uranyum tuzunu hava yağmurlu olduğu için çekmecesine koydu ve birkaç gün sonra çıkarıp banyo etti. Sonra böyle bir manzara ile karşılaştı. Bu nasıl olabilirdi? Kendi kendine ışın yayabilen tuhaf bir madde? İnanamadı...
Becquerel bu gizemli ışınlara "Becquerel ışınları" adını verdi. Ancak aradan çok fazla zaman geçmeden biri bu ismi değiştirecekti; Marie Skłodowska Curie. Becquerel'in doktora öğrencisi. Bu bilim insanının adını söylemek bile tüylerimi diken diken ediyor...
O'nun hayatı ve çalışmaları bu yazıya sığmaz. O yüzden hemen geçeceğim. İlgilenenler için kısa hayatı; http://www.reitix.com/Makaleler/Marie-Curie-nin-Hayati/ID=940 …
Curie, Becquerel'in keşfettiği ışınları "Radyoaktif ışınlar" bu ışınları yayabilen maddeleri ise "Radyoaktif Maddeler" olarak adlandırdı. Radyoaktivite üzerine çalışmalarında tuttuğu notlar. Hâlâ radyoaktiftir bu defter, korumasız inceletmezler, kurşun muhafazada saklanır.
Şimdi de klasik fiziğin kabusu olan bir diğer problemi ele alacağız; kara cisim problemi.
Bir sıcaklığa sahip olan bütün nesneler ışıma yaparlar. Yeter ki mutlak sıfır noktasından (-273,15 °C ya da 0 Kelvin) sıcak olsunlar. E biz niye görmüyoruz bu ışınları? Çünkü yeterince sıcak oldukları vakit "görünür ışık" yayarlar. Onun dışında göremezsiniz. Gözünüz ~12°C sıcaklıkta yayılan ışınları da görebilseydi (kızılötesi ışınlar) devekuşlarını böyle görebilirdik.
Ya da yeterince ısınmış demir bir yay artık gözümüz tarafından algılanabilen ışınlar yaymaya başlar.
İdeal bir kara cisim, üzerine düşen ışığı mükemmel bir şekilde soğurur. Bu yüzden siyah görünür. Peki ısıtılırsa ne olur? Bu kez de ışık, yani enerji yaymaya başlar. Yukarıdaki örneklerde görüldüğü gibi kara cismin sıcaklığına bağlı olarak. Bu ışınların enerjisi değişebilir. Dolayısıyla yeterince sıcaksa, görünmeyen ışınlara ek olarak görünür ışınlar da yaymaya başlar.
Peki, burada "PROBLEM" nedir? Problem şu; klasik EM dalga yaklaşımı (formülleri) sıcaklık arttıkça yayılan ışınımın enerjisi de doğrusal olarak sürekli artar diyor. Buna bir limit, sınırlama getirmiyor. Ne kadar sıcaksa o kadar yüksek enerjili ışınlar salınır. Bu durumda bir şömineden yayılan toplam ısı enerjisinin tamamı en yüksek enerjili ışınlar yoluyla yayılır ve bizi anında kavururdu?
Ama biliyoruz ki, şöminenin önünde keyifle oturup kahvemizi içip kitabımızı okuyabiliyoruz? Neler oluyor? O zamanın Klasik Fizikçileri bu çıkmaza "Morötesi Felaket" adını vermişlerdi. Morötesi denmesi tesadüf değil elbet.
Morötesi ışınlar yüksek enerjili ışınlardır. Yani şömine enerjisinin tamamını Morötesi olarak yapıp tüketmek yerine niçin orta enerjili seviyelerde (görünür bölge) en fazla, düşük (kızılötesi) ve yüksek enerjili (morötesi) ise daha az yapıyordu? Bizim kahve ve kitap keyfimiz bozulmasın diye böyle birşey yapıyor olamaz değil mi? :-)
Başka bir örnek vereyim;
Otoyolda hız sınırı 120 iken arabaların büyük çoğunluğu ortalama 100 ile giderken pek azı hız limitini aşar, pek azı ise gereğinden fazla yavaş gider. Hız limitini (sıcaklığı) 140 yaparsak yine birkaç araba hız sınırını aşacak ama ortalama değer trafiğin akışını bozmayacak şekilde (örneğin 105) sabit kalacak. Yani siz hız sınırını (sıcaklığı) ne kadar arttırırsanız arttırın ortalama hızlar hep hız sınırı değerinden çok daha düşük olacaktır. Bu şöminenin neden bizi kavurmadığını açıklar.
Ancak, o zamanın klasik fizik yaklaşımı hız sınırı arttıkça sanki bütün arabalar hız sınırına yakın veya üzerinde hareket etmek zorundaymış gibi bir resim sunuyordu bize. Ancak doğanın da bir "trafik polisi" vardı: KUANTUM DOĞASI.
Bu görünmez polis sürekli olarak trafik akışının (Enerjinin salınımının) güvenli bir aralıkta olmasına neden oluyordu.
Ludwig Boltzmann. Gazların kinetik teorisi üzerine çalıştı. Kapalı bir kapta uçuşan gaz moleküllerinin enerjisinin sıcaklığa bağlı olarak değiştiğini gösterdi.
Ancak moleküllerin her birinin enerjisini kestirmek imkansızdı. Bunun yerine "ortalama kinetik enerji" kavramından bahsetmek daha doğru olurdu. Yani herhangi bir sıcaklıkta moleküllerin en fazla yığılma gösterdiği (tepe noktası) yer ortalama enerji üzerinde belirleyicidir.
Dikkat ederseniz grafikte 1000-1500 hız aralığında çok fazla molekül var.
Ancak 500'den az veya 2500'den fazla moleküller de var ama sayıları çok az değil mi? Bu istatistiksel dağılımla konumuzun ne ilgisi var diyenler şömineden yayılan ışınım enerjisi konusunu tekrar düşünmeliler; YAYILAN ENERJİNİN BÜYÜK BİR KISMI ORTA ENERJİLİ IŞINLAR YOLUYLA, PEK AZI İSE ÇOK YÜKSEK VEYA ÇOK DÜŞÜK ENERJİLİ IŞINLARLA SALINMAKTADIR. Tıpkı Boltzmann'ın kapalı kapta hareket eden moleküllerinin uyduğu bir istatistiğe benzer şekilde! Buradan MAX PLANCK KUANTUM TEORİSİNİN DOĞUMUNU GERÇEKLEŞTİRECEKTİ!
Hepimiz doğayı bir süreklilik algısı ile deneyimliyoruz. Etrafınıza bir bakın, her şey kesintisiz akıyor değil mi? Ancak iş doğayı en küçük ölçeklerde incelemeye gelince hiçbir şey sürekli değildi. Herşey kesikli, ayrık, öbekli yapıdaydı. ENERJİ BİLE!
Bu kavrayışı, bir Alman dehası olan Max Planck'a borçluyuz. Tarihler 1900 yılını gösterirken, hiçbir şey artık eskisi gibi olmayacaktı.
Planck şayet enerjiyi "sürekli bir akış gösteren fenomen" olarak değil de, tıpkı Boltzmann'ın gaz molekülleri gibi "AYRI BİRİMLER" halinde bir kaynaktan yayınlandığını düşünürsek, o zaman şöminenin neden bizi kavurmadığı anlaşılacaktı!
Evet! Bu muazzam bir fikirdir! Enerjiyi minik, miniminnacık parçacıklar halinde yayıldığını varsaymak: QUANTA'LAR HALİNDE!!! J
Enerji süreklilik, yani devamlı bir akış gösteren fenomen olsaydı, klasik fizik gereği şömine bizi kavururdu çünkü şöminenin bütün enerjisi en yüksek (frekansı en yüksek) enerjili ışınlar yoluyla yayılacaktı ve bizi kızarmış tavuğa çevirecekti!
Ama enerjiyi ayrık birimler (Boltzmann'ın gaz molekülleri gibi) halinde ele alırsak, o zaman şöminenin toplam enerjisi sadece en yüksek frekanstaki ışınlardan değil, aksine orta frekanslı (enerjili) ışınların en fazla olduğu bir dağılım gösterecekti!
Planck'ın formülü ve eğrisi. Boltzmann'ın moleküllerinin istatistiksel dağılım grafiği ile neredeyse aynı değil mi? :-)
Ne büyük ironi değil mi? Kuantum "fikrinin" bir klasik fizikçinin (Boltzmann) bakış açısının apayrı bir olaya uyarlanmasıyla doğması...
Hayal edin şimdi lütfen... Şu anda üzerinize güneşten gelen saniyede Trilyon x Trilyon x Trilyon tane parçacık çarpıyor. QUANTALAR! Yani aslında üzerimize her saniye muazzam sayıda YAĞMUR GİBİ YAĞAN QUANTA'LAR var. Bu QUANTA'lar enerjinin "YAĞMUR DAMLALARI"...
Her bir Quanta'nın enerjisi, sadece frekansı ile (dolayısıyla dalgaboyu) orantılıdır. h ise frekansı enerjiye çeviren "sabit kur'dur".
Buraya geleceğimizi daha önce söylemiştim unutmadınız değil mi?
İleride göreceğiz, bir ışın demetinin enerjisi sadece frekansı (dolayısıyla dalgaboyu) ile orantılıdır.
Şimdi son kısmı özet geçip iyice oturtalım; yanan bir şömineden çıkan enerji aslında devasa bir QUANTA YAĞMURU şeklindedir. Yağmur bulutundan (yani aslında odunun toplam enerjisi) ayrılan her damlanın (quanta) büyüklüğü (frekansı ve enerjisi) aynı değildir.
Bazı damlalar fazla iridir (bazı quantalar çok yüksek frekanslıdır -yani bizi kızarmış tavuk yapacak) bazı damlalar orta büyüklüktedir, bazı damlalarsa çok küçüktür (frekansı ve enerjisi en düşük quantalar). Burada ayrılan damlaların çok büyük bir kısmının "orta büyüklükte" olduğunu ifade etmeye çalışıyoruz. Dolayısıyla istatistiki olarak karşımıza kahve ve kitap keyfi yapmamızı sağlayan bir manzara çıkıyor.
Şayet bu Quanta doğası olmasaydı, buluttaki bütün su (odunun tüm yanma enerjisi) tek bir dev damla hâlinde (en yüksek frekansta ışınlar) üzerimize boşalır, belki boynumuzu kırar atardı (ışınlar bizi kızarmış tavuğa çevirirdi). Umarım bu karşılıklı benzetmeler faydalı olmuştur.
Quanta fikri (bakın Kuantum demiyorum çünkü bu ismi ileride bir başkası söyleyecek) Kuantum Teorisinin bel kemiği, temelidir.
Unuttum sanmayın, Fotoelektrik efektin gizemi ve Radyoaktivite bilmecelerini de bu temel üzerine inşa edeceğiz.
Işığın Emisyon ve Absopsiyon çizgilerini bu bakış açısıyla atomlara uygulayabileceğimizi göreceğiz (daha önce ipucunu vermiştim : Bohr atomu).
Planck'ın Quanta devriminden yaklaşık 5 yıl sonra dünyanın gördüğü en büyük dehalardan biri bunu büyük bir sorunun çözümüne uygulayacaktı
Albert Einstein... Yıl 1905. Max Planck'ın editörlüğünü yaptığı Alman Annalen der Physik dergisine 3 adet makale gönderir.
Makalelerden biri Özel Görelilik, ikincisi Brown hareketleri (atom-moleküller üzerine) ve üçüncü ve bizi ilgilendiren makale ise Fotoelektrik Olayın Açıklaması üzerine idi. Max Planck makaleleri okudu ve dehşet içinde kaldı... Artık Fizik, başka bir Fizik olmuştu.
Şanslıyız, bu konuda daha önce seviyemize çok uygun bir zincir yapmıştım. Buradan yakınız; :-)
Emekleme çağındaki kuantum kuramı Einstein'in parlak zekâsıyla birleşince fizikçilerin kâbusu fotoelektrik etki zarif bir çözüme kavuşmuştur.
Bu noktadan itibaren yazının sonuna dek okuyacaklarınız Alice'in harikalar diyarına değil, Kuantum dünyasına ait şeyler olacaktır.
Bazı şeyler mantığınızı fazlasıyla zorlayacaktır, bazı şeylerse aşırı fantastik gelebilir; küçüklerin dünyasında gerçek olan şeyler! Elimden geldiğince sağduyunuza hitap etmeye çalışacağım.Bazı yerlerde konu felsefeye uzanabilir bazı yerlerde mistisizm çağrıştırabilir. Ama şundan emin olun, konu tamamen bilimsel bağlamı ile işlenecektir. Lütfen buna göre cevap, fikir ve yorum getiriniz.
Şimdi Fotoelektrik etki ile devam ediyoruz. Ne yapmış bu Einstein? Fotoelektrik yazısında okudunuz, ben sonuçlarını anlatayım...
Einstein ışığın dalga modelini (hani Young'un çift yarık deneyiyle bize dalga olduğunu ispatladığı var ya) bir kenara fırlatıp ışığın foton adı verilen taneciklerden oluştuğunu öne sürmüştür. Nasıl yani? Bir dakika kardeşim, çift yarık deneyi dalga olduğunu ispatlıyorken nasıl bir başka deney onun tanecik olduğunu ispatlar? Dalga başka bir şey, tanecik başka... Ya odur, ya da o değil mi?
Değil... Doğa bize ışığın hem dalga hem tanecik olduğunu söylüyor. Yani hem elmayım, hem de uzaktan kumanda gibi bir şey. İkisi birden.
Dalga-Parçacık ikiliğini ileride tekrar ele alacağız. Kara cisim ve Fotoelektrik sorunlarını çözdük. Sırada tayf çizgileri var.
Hatırlarsanız Bohr atomunda kısaca üzerinden geçmiştik. Şimdi azıcık detaylı bakalım mı?
Bohr, elektronları farklı enerji seviyelerine (n) yerleştirmeyi seçti. Çekirdeğe en yakın ve enerjisi en düşük seviye n=1' dir.
n değeri arttıkça,katmanın enerjisi artar. Şimdi size soru; n=1 katmanındaki bir elektron n=2 (veya 3,4...) seviyesine çıkarabilir mi? Cevap evet çıkabilir, "dışarıdan aradaki enerji farkı kadar enerji kazanması şartıyla". Peki bu enerjiyi nerden bulacak? "QUANTA'DAN"!
Diyelim ki n=1 seviyesindeki elektrona bir quanta çarptı. quanta taşıdığı enerjiyi elektrona aktarır ve onun yüksek enerjili bir katmana sıçramasına neden olur, hangi katmana çıkacağı ise quanta'dan aldığı enerjinin miktarına bağlıdır. Yeterince yüksek ise elektron tamamen atomdan kopup fırlayabilir de. (Fotoelektrik etkideki gibi) Zaten ışığın tayfinda karanlık çizgiler bu yüzden oluşur.
Aslında her bir karanlık çizgi, atom tarafından soğurulan bir quanta'nın boşalttığı yeri temsil eder. Çünkü elektrona çarptı ve yok oldu. Olaya tersten de bakabiliriz. Yüksek enerjiye sıçrayan elektron tekrar düşük enerjili katmanlara dönebilir. O zaman ne olur?
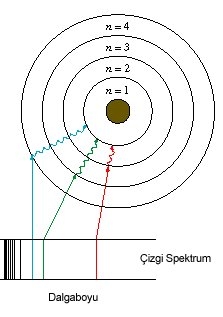
Evet, o zaman da aradaki enerji farkı kadar quanta yani ışık fotonu yayınlanır. Bakın bu görselde elektron n=3'ten n=1'e düşerken yeşil renge karşılık gelen enerjide (frekansta) quanta salınırken, 2'den 1'e düşen bir elektron kırmızı rengin frekansında enerji salıyor.
4'ten 1'e düşerken salınan ışığın frekansı en yüksek yani enerjisi biraz daha büyüktür, çünkü katman farkı daha büyük farkettiniz mi?
Buradan mavi ışığın enerjisinin yeşil ışıktan, yeşil ışığın da kırmızı ışıktan daha büyük olduğunu çıkarabiliriz. Bakın aşağıda elektronları yüksek enerji katmanlarından düşük enerjili katmanlara "düşen" atomların yaydığı ve "görünür bölgeye" ait olan emisyon tayflarını görüyorsunuz.
Soğurdukları quantalar vardı ya, şimdi onları geri serbest bırakıyorlar J
Peki ya elektron çok daha yüksek enerjili katmanlardan daha düşük enerjili katmanlara düşerse? Bu resmi hatırladınız değil mi? Wilhelm Röntgen'in karısının parmak iskeletleri. Peki nasıl olmuştu bu onu hatırladınız mı?
Röntgen, adına "X ışınları" dediği çok yüksek enerjili ışınlar keşfetmişti. Sonra karısı elini bu ışınların önüne koyunca bu film çıktı.
Demek ki neymiş? Aslında Röntgen, atomlarda çok yüksek geçiş enerjisine tekabül eden elektron geçişleri keşfetmiş!
X ışınlarının spektrumda ne kadar yüksek enerjili (frekanslı) bölgede olduğuna bir bakın! (Görünür bölgenin solunda)
Işık/atom ilişkisi, enerjinin belli büyüklükte paketler (quanta) halinde alınıp verildiğinin güzel bir örneğidir. Bohr'un atom modeli bu anlamda önemli bir problemi çözmüştü. Ama çok da sevinemedi Bohr. Sorunların biri çözüldü derken diğeri başlıyordu.
Bohr'un atom teorisi tek elektronlu hidrojeni (ve bazı iyonları) başarıyla açıklarken, çok elektronlu atomlarda çaresiz durumlara düşüyordu.
Zeeman efekti diye bir bela vardı mesela. Elektrona ait bir enerji geçişi normalde tek çizgi vermesi gerekirken manyetik alan içinde birden fazla geçiş çizgisi veriyordu.
Yani diyelim ki Bohr'un atom modeli 12 katlı bir bina olsun. Her katın enerjisi farklı. Her katta elektronlar var. Bir elektron 7. kattan 1. kata düşüyorsa, "belli ve tek bir hızla" çarpar değil mi? Ama Zeeman olayında elektron manyetik alana tabi iken 7. kattan 1. kata düşünce üç farklı hızla yere çarpabiliyor! Sanki 7. katın içinde de ayrı ayrı katlar bağımsız katlar varmış gibi! Yeni bir atom modeline ihtiyaç vardı. Ama kuramsal ilerleme gerekiyordu. İlerleyelim o zaman? :-)
Arthur Compton. Yıl 1923. Einstein ışığın "quanta" yani "foton" yani "tanecik" olduğunu söylemesinin üzerinden 18 yıl geçmiştir.
Compton, elektronları fotonlarla bombardıman ederek sonuçları inceliyordu. Fotoelektrik etkiden bildiğiniz gibi elektrona çarpan foton, onun atomdan sökülmesine neden olabiliyordu. Peki ya çarpıp yoluna devam ediyorsa? Tıpkı bir bilardo topuna çarpıp sekerek devam eden diğer bilardo topu gibi? Enerjisini biraz kaybederdi ama yoluna devam edebilirdi? Evet, sonuçlar aynen bunu gösteriyordu...
Bakın, resimde aynen bu oluyor. Gelen foton kısa dalgaboyu (mavi) ve yüksek enerji ve frekansta. Elektrona toslayınca bir açı ile saçılıyor.
Saçılan fotonun dalgaboyu uzamış (kırmızıya kaymış) ve dolayısıyla enerjisi ve frekansı azalmış gördünüz değil mi? Nereye gitmiş bu "fark enerjisi?" Tabi ki orada mazlum mazlum otururken bir anda fotondan yumruk yiyen elektrona. :-)
Bu olaya Compton saçılması denir. Ve ışığın tanecik karakteri taşıdığının diğer bir örneğidir. Dalga modeli nakavt mı oluyor ne??
Cevap; hayır. Dalganın nakavt olmaya hiç mi hiç niyeti yoktu. Bir Fransız asilzadesi her şeyi yine allak bullak etti; Louis de Broglie...
Broglie, Einstein'in E=mc2 (madde enerjidir) formülü ve Planck'ın E=hf (enerji quanta'dır) formüllerini eşitleyip ilginç bir sonuca ulaştı;
Broglie şunu iddia ediyordu artık; HIZI ve KÜTLESİ OLAN HERŞEYE EŞLİK EDEN BİR DALGA VARDIR! :-) Ne olursa olsun, fark etmez!
Formülde kendi kütlenizi gram olarak yazıp kendi dalgaboyunuzu bile bulabilirsiniz :-) (ama çok ufak bir sayı çıkar, anlamsız gelebilir)
Broglie tozu dumana kattı. Diyordu ki, dalga ve parçacık et ile tırnak gibidir, ayıramazsınız!! Fizik çığırından çıkmıştı artık.
Broglie'nin bu tezi elektronların neden "belirli" enerji seviyelerinde (çekirdekten uzaklık) olduğunu da tatminkar açıklıyordu.
Broglie'nin bu yaklaşımı bize, dalga/parçacık ikiliğini kabul edip sindirmemizden başka bir seçenek olmadığını gösterdi.
Young'ın çift yarık deneyini detaylı ele aldığımızda bu doğa üzerine daha keskin fikirler edineceğiz. Ama birazcık daha yolumuz var.
Şimdi, Thomson bize elektronun bir tanecik olduğunu söylemişti. Broglie ise onun aynı zamanda bir dalga karakteri olduğunu iddia ediyor
Size bir taneciğin uzayda yerini net olarak söyleyebilirim. Peki dalganın yeri ne demek? Dalganın bir "yeri" var mıdır?
Erwin Schrödinger. Broglie'den aldığı pası gol yapmak için gereken yetenek onda fazlasıyla vardı.
Schrödinger, elektronun dalga doğası gereği onun tam bir konumundan bahsetmektense KONUMUNUN OLASILIĞINDAN bahsetmeyi seçti. Bu, sevgilinizin size net bir buluşma noktası vermesindense "şu kadar ihtimalle şu mağazanın önünde olacağım" demesi gibi birşey. Tabii sevgilinizi örneğin %60 ihtimalle orada bulmanız gerekiyorsa, %40 ihtimalle de mağazanın önünde bulamayacağınız anlamına geliyor.
Ancak Schrödinger’in %100 ihtimalle sevgilinizin şehir içinde bir yerde sizi beklediğinin garantisini de verdiğini söyleyelim. Arayın onu :-)
Bakın mesela burada bir elektron "çok büyük ihtimalle" çekirdeğin 0,53 A° kadar uzağında (tepe noktası maksimum olasılık) :-)
Şu durumda artık elektronun konumu için bir "olasılık haritası" (Fizikçiler ORBİTAL der) çıkarılabilir değil mi?
Bakın yukarıdaki gif resimde çekirdeğe en yakın elektronun bulunma olasılığı modellenmiş. Koyu bölgeler (iç kısım) olasılığın yüksek, yani elektrona "denk gelme" ihtimalimizin en fazla olduğu yerler, dışa doğru olasılık "seyrekleşiyor" yani azalıyor.
Bakın burada başka bir elektron için "olasılık haritası" çıkarılmış. (ilgi duyanlar için bu "d" orbitali diyagramıdır)
Bunlar da başka olasılık haritaları yani orbitaller. Hepiniz Lise Fizik/Kimyasından bunları bilirsiniz.
Bunlar, Schrödinger'in dalga fonksiyonu denklemlerinin çözümlenmesi sonucu ortaya çıkan ve elektronların konum olasılıklarını gösteren "uzay bölgeleridir".
Kuantum ilkelerinin geçerli olduğu bir dünyada kesinlikten bahsedilemeyeceğinin ilk işaret fişeğini Schrödinger fırlattı diyebiliriz. Bu dünyada "ihtimaller" sözkonusuydu. Sadece elektronun konum ihtimaliyle sınırlı değildi durum; ne zaman "sıçrama" yapacağı da bir olasılık konusuydu.Yani üst enerjili bir seviyeye çıkarılmış elektronun ne zaman temel hâle döneceği hakkında kesin bir şey söylenemez
Werner Heisenberg. Olasılık fikri daha sindirilmemişken ortalığı velveleye verecek başka bir şey daha attı ortaya: BELİRSİZLİK...
Bu ilkeye göre bir parçacığın konumu ve momentumu (hızı gibi de düşünebilirsiniz) asla tam olarak ölçülemez! Konumu ne kadar hassas belirlerseniz, momentumu o kadar belirsizleşir. Momentumunu hassas ölçeceğim derseniz, bu kez de konum belirsizleşir. Konum (x) ile momentumun (p) çarpımı daima belli bir miktar (eşitliğin sağı) belirsizlikten büyük olmak zorunda!
Bu şuna benziyor; hareket halinde bir aracın hızını ne kadar hassas ölçersek nereye gittiğinin belirsizliği büyüyor, nereye gittiğini hassas bir şekilde ölçecek olsak bu kez de hızı aynı derecede belirsizleşiyor. Size klasik fiziğin bakışıyla anlatayım.
Klasik fiziğe verin bir parçacığın ilk hızını ve ona etki eden kuvvetleri, size o parçacığın geleceğini söylesin! Ama aynı şey küçüklerin dünyasında olmuyordu! Heisenberg diye biri çıkıp "bunu yapamazsınız, parçacığa ait fiziksel veriler belirsizlik içerir, dolayısıyla onun ne "şimdi"sini ne de "geleceğini" tahmin edemezsiniz. Katı neden-sonuç ilişkisi (deterministik doğa) içinde ele alınan fiziksel anlayış artık bir enkazdan ibaretti. Laplace'ın şeytanı ölmüştü...
Hepiniz çarpma işleminde değişme özelliği olduğunu bilirsiniz. a.b=b.a' dır. Dolayısıyla a.b-b.a = 0'dır diyebiliriz değil mi?
Şimdi, ben bir parçacığın bir no'lu özelliğini p olarak ölçmüş olayım. Arkasından iki no'lu özelliği ise q olarak ölçmüş olayım. Sırayla ölçüm sonuçlarının çarpımını yazıyorum; p.q Sorun yok değil mi?
Şimdi işlemi tersten yapıyorum. Önce iki no'lu özelliği ölçüyorum ve q buluyorum. Ardından bir no'lu özelliği ölçüyorum ve p buluyorum.
Yine sırayla ölçüm sonuçlarının çarpımını yazıyorum; q.p Sorun yok değil mi?
Burası tuhaf bir dünya. Hangi özelliği önce ölçtüğünüz bile diğerinin sonucunu etkiliyor! Dolayısıyla p.q ile q.p aynı değer değil!
Bu neye benziyor biliyor musunuz, diyelim ki 1 adet 70 cc Johnie Walker Red Label viskiniz var ve bunun alkol oranını bulmak istiyoruz. Diyelim ki önce alkol miktarını sonra da su miktarını ayrı ayrı bulup alkol oranını hesapladınız; %60 alkol olsun. Şimdi de aynı şişeyi bu ama bu kez önce su, arkasından alkol miktarını belirleyecek şekilde işlem yapalım. Sonuç %60 alkol çıkmıyor...
Biliyorum, şu anda ekrana donuk ve şaşkın bir şekilde bakıyorsunuz. Ben size Alice'in harikalar diyarında olmadığımızı baştan söylemiştim.
Max Born bu tuhaf olayı -Heisenberg ile birlikte- matris çarpımları olarak göstererek Schrödinger'in dalga mekaniğine alternatif olarak "Matris Mekaniği"ni kurdu.
Bu arada Born ilk kez 1924'te "Über Quantenmechanik" (Kuantum mekaniği üzerine) makale yayınlamış yani "Kuantum" ifadesini ilk kez bilimsel bir yayında kullanmıştır.
Artık özgürce KUANTUM diyebiliriz yani :-)
Schrödinger bayraktarlığında artık atomun "KUANTUM MODELİ" belirmeye başlamıştı. Kesin çizgileri olmayan, bulut gibi puslu bir şeydi... Schrödinger, Bohr modelinin çıkmazlarını büyük oranda çözdü. Zeeman efekti vardı ya; hani "kat içinde kat var gibi" dediğim, Schrödinger elektronlar için 3 ayrı "kuantum özelliği" tanımladı. Böylece elektronlar aynı katta olsalar bile farklı enerjilere sahip olabiliyordu
Ancak ufak bi sıkıntı daha vardı. Sanki 4. bir kuantum özelliği daha eksik gibiydi. Ve Wolfgang Pauli sahne aldı...
Dedi ki; "durun yoldaşlar, bir koltuğa iki karpuz sığmaz".. Kuantum diliyle söylersek; aynı enerjiye sahip 2 elektron (yani 3 kuantum özelliği aynı olan) birbirini başka bir yönden dışlamak zorundadır. Bu yüzden 4. bir kuantum sayısı daha gerekir.
Buna "Pauli Dışarılama ilkesi" diyoruz. Bunun gündelik dilde anlamı şudur; bir atomda bulunan hiçbir parçacık "aynı" davranamaz. Bu yüzden evrende çeşit çeşit element var, bu yüzden yıldızlar parlıyor, ve bu yüzden siz bunları okuyorsunuz.
Geldiğimiz noktada olasılıkçı ve belirsizlik içeren bu durum bir devi içten içe rahatsız ediyordu; EİNSTEİN. Einstein 1926'da Born'a (Bohr değil) yazdığı mektuptan bir pasaj. "Tanrı zar atmaz'ın" gerçek versiyonu.
Einstein özetle şunu söylüyordu; bu Kuantum fikri çok ilginç ve kapsamlı şeyler söylüyor ancak bu bana pek inandırıcı gelmiyor ve bu şey bize "yaşlı adamın" (Tanrıyı kastediyor :-) ) sırrını verecek bir yaklaşım gibi durmuyor. Yani her şekilde ben tanrının zar atmayacağı fikrini taşıyorum" Yani tanrının şans ve olasılıkla işi olmaz diyordu yaşlı kurt. Ama Einstein daha neye bulaştığını bilmiyordu.
Buraya kadar olan kısımda bizi "quanta"lardan "quantum"a getiren fikri toparlamak ve bağlantıyı keşfetmenizi istiyorum.
Planck ve Einstein'in quanta fikri fiziksel bir "ayrıklık" ifade ediyordu. Bu ayrıklık doğanın sürekli değil kesikli parçalardan oluşan devamlı bir akışa sahip olmasına neden oluyordu. Tıpkı devamlı algılanan bir film sahnesinin temelde tek tek fotoğraf karelerinin aslında hızla geçip gitmesi yani "parçalardan" meydana geliyor olması gibi.
Bu kesiklilik, parçalılık hali atom ve atomaltı parçacıkların bütün fiziksel özelliklerine yansımış haldedir. Bir elektron için yukarıda 4 kuantum sayısından bahsettik mesela. Mesela bunlardan biri momentumun kuantumlanmasıdır. Yani doğa elektrona "sen yalnızca şu momentum değerini veya bunun tam katlarını alabilirsin" diyor. Bakın bu bir kesiklilik yani süreksizlik ifade eden bir yaklaşımdır.
Anlamanızı kolaylaştırmak için örnek vereyim; arabanız elektron olsaydı gaza bastığınızda hızı (dolayısıyla momentumu ) sadece belli değerleri veya onun katlarını alabilirdi. Örneğin araba ilk anda 10km/s ile zıplar ardından orantı sabitine (Planck sabiti) bağlı olarak mesela 10'dan bir anda ibre 20'ye, 20'den bir anda 30'a gibi hızınız 10'ar 10'ar artardı. Yani ibreniz kesinlikle aradaki değerleri almazdı. Bu hızın tıpkı quanta'lar gibi belirli yani kesikli değer alabileceği yani Kuantum özelliği gösterebileceği anlamına geliyor.
Yine benzetme kuralım, TV ekranlarında görüntü uzaktan sürekli gibi algılansa da aslında en yakından bakılınca piksellerden oluştuğu görülür.
Yani küçük, süreksiz birimler! Pikseller TV'nin quantalarıdır!
İşte Kuantum kelimesinin fiziksel anlamı ve quanta ile bağlantısı budur! Fiziksel her özellik quantalaşmıştır yani kuantize olmuştur; yani kuantum özelliği gösterir! Bu kesiklilik süreksizlik halini kendi dünyamızda farkedemiyoruz çünkü sabiti çok çok küçük!
Şayet Planck sabiti (h) daha büyük olsaydı, yaptığımız herşey farkedilir şekilde belli bir büyüklüğün katları halinde olurdu! :-)
Örneğin kafamızı 90° sağa çevirdiğinizde bunu sürekli değil, örneğin 3 parça halinde 30° derecelik açılarla yapardık belki de :-)
Burada ne yapmış olduk? Dönme hareketini "kuantize" etmiş yani Kuantum özelliğine bürümüş olduk.
Bu kısmın ana fikri, küçüklerin dünyasında fiziksel bir büyüklük sadece belli bir en küçük değer ve onun katları şeklinde ifade edilir. Mesela 0 ile 1 arasında sonsuz sayı vardır. Reel sayılar yani. Reel sayılar kuantize değildir. "Doğal sayılar" ise kuantizedir. Çünkü sadece 0,1,2,3.. gibi belli değerler ve onların tam sayı katları (birer birer artış) şeklinde artış gösteriyor.
Bu bölümü yazıya eklememin sebebi benim için çok önemli idi. Çünkü öğrenme "BAĞLANTILAR KURARAK" gerçekleşir.
Şimdi Kopenhag'a, Bohr'un yanına gitme zamanı. Bizi çok ama çok ilginç hikayeler bekliyor...
4.Bölüm: Kuantum Mekaniği Kopenhag Yorumu; "İki Dünyanın Savaşı"
Yıl 1930.. Önde ortada oturan Niels Bohr. Solundaki ise Kopenhag üniversitesinden asistanlığını da yapmış olan Werner Heisenberg.
Kopenhag yorumu Bohr-Heisenberg'in 1920'li yıllar boyunca geliştirdikleri, değerlendirdikleri düşünceler bütünüdür. "Kopenhag yorumu" adında basılı bir eser yoktur, ancak Kopenhag yorumu denince bu ikilinin kuantum mekaniğini yorumlama biçimleri anlaşılır
Neyse, kelimenin etimolojisini bir kenara bırakıp konuya gelelim. Nedir bu yorum? İlkeleri nelerdir? Ne söyler?
İlke1: Bir sistem, üzerinde ölçüm yapılana dek bu sistem olası bütün durumları (ihtimallerin) içinde barındıran ya da başka deyişle bütün bu durumların üst üste bindiği bir "karışım" halindedir. Buna modern dilde "süperpozisyon" denir.
Temsilen, havada dönen bir madeni para "süperpoze" haldedir, yani olası iki durumu da (yazı ve tura) içerir.
Ne zaman ki avucunuza düşer ve bir ölçüm yaparsınız, işte o zaman gerçekliği ortaya çıkar. Buna da "dalga fonksiyonu çöküşü" denir.
Bu ilke üzerine uzun konuşacağız. Çünkü inanılmaz sonuçları var. Bir defa "gözlemciyi" merkeze alıyor, onu "gerçekliğin belirleyicisi" sıfatına kavuşturuyor. Başka bir örnek. Parkta oynayan bir çocuk siz onun ne yaptığını ölçene dek, yani onu gözleyene dek aslında hem kaykay'da kayıyor, hem tahterevallide sallanıyor, hem salıncakta sallanıyor kısaca parkta yapılabilecek ne varsa hepsini yapıyor varsayılır. (Cocuk superpoze) Siz ona baktığınız anda bütün ihtimaller tek bir duruma çöker: çocuk bankta oturuyor. :-)
Elbette bu, kuantum mekaniğinin gündelik hayatta geçerli olması durumunda ortaya çıkan senaryo. Elbette çocuk aynı anda her şeyi yapamaz
İlke2: "Bir sistemin tüm fiziksel özellikleri tam bir kesinlikle saptanamaz, birinin kesinliği diğerlerinin belirsizliğine yol açar" Bu ilke farkettiğiniz gibi, Kuantum mekaniğinin kalbi olan Heisenberg'in Belirsizlik ilkesidir.
Werner Heisenberg. Olasılık fikri daha sindirilmemişken ortalığı velveleye verecek başka bir şey daha attı ortaya: BELİRSİZLİK...
Kopenhag yorumunun en can alıcı ilkesi belirsizlik ilkesidir. Birinci ilke ile uyumlu çalışımakla birlikte, bir de üzerine ölçümde ölçülen fiziksel özelliğin diğer fiziksel özellikler üzerinde kaçınılmaz bir "sapma" yarattığını iddia etmektedir.
Örneğin yuvarlanan bir bilyenin "şu anda nerede" olduğu bilgisi ölçüm gerektirir. Ölçüm ise bilyeden foton (ışık) ayrılmasını gerektirir. Siz fotonu gördüğünüzde konumu net bir şekilde bilirsiniz, ancak başka bir şey belirsizleşmiştir: BİLYENİN HIZI!
İyi de nasıl değişir? Şöyle, namludan fırlayan mermi, tüfeği nasıl geri teptiriyor ve ona ters yönde bir itme kuvveti yaratıyorsa bilyeden ayrılıp gözümüze doğru hareket eden ve bize bilyenin konumunun bilgisini taşıyan foton da, bilyeyi "iter" ve onun hızını belirsizleştirir.Yani,siz konumu tam ölçeceğim derken bilyenin hızı değişmiş oldu. Bu işlemi tersten yapsanız, yani hızı kesin olarak ölçmek isteseydiniz bu kez de bilyenin konumu hakkında net bir bilgiye sahip olma şansını kaybedecektik.
İlke3: Mikro dünya mikro yasalarıyla (Kuantum Mekaniği), makro dünya makro yasalarıyla (Klasik Mekanik) açıklanabilir. Bohr; bu iki dünyayı ayrı değerlendirmek gerektiğini, aksi halde (parkta oynayan çocuk gibi) anlamsız sonuçlar çıkacağını düşünür. Einstein ise buna şiddetle itiraz eder: Hayır kardeşim, makro dünyada ne geçerli ise mikro dünyada da o geçerli olmak zorunda!
"Sizin dünyanızdaki (mikro dünya) tuhaflıklar, teorinizin (kuantum) henüz tam olmayışından kaynaklanır" der Einstein. (Samimi dille söyleyelim); kısaca, Einstein'e göre olasılıkmış belirsizlikmiş falan bunlar hikaye masal şeyler. Bohr ve Heisenberg'in anlamsız kuruntularından ibaret hepsi. İster Jüpiter ister Proton fark etmez, onları ölçelim veya ölçmeyelim, belirli ve her şeyden bağımsız sahip oldukları "belirli fiziksel özellikleri" vardır. "İki dünya savaşı" şiddetlenmeye başlamıştır.
Einstein bu itirazlarını 2 arkadaşıyla birlikte bilim dünyasına haykırır: EPR paradoksu...
Bu paradoks, 2 ve 3 numaralı ilkelere şiddetli bir itirazdır. Makalede bir deney önerilmese de bir çıkmaza işaret edilir.
Einstein "mealen" şunu der; (yine samimi ağızla yazacağım); YAHU BOHR KARDEŞ ETME EYLEME BU YOL YOL DEĞİL, YOL YAKINKEN DÖN İSTERSEN. BAK SİZİN BU TUHAF İDDİALARINIZIN BİR ASLI ASTARI YOK, TAMAMEN HESABA KATMADIĞINIZ BELKİ DE KATILAMAYAN BİR TAKIM "GİZLİ DEĞİŞKENLER" OLABİLİR, VE BU GİZLİ DEĞİŞKENLERİ HESABA KATMADIĞINIZ İÇİNDE BÖYLE TUHAF TUHAF ŞEYLER İDDİA EDİYORSUNUZ. ASLINDA BELİRSİZ VE İHTİMAL İÇEREN HİÇBİR DURUM YOK ORTADA" der.
EPR çıkmazı bir çift eldiven örneği ile güzel anlatılabilir. Bir çift eldivenden her bir tekini birisi iki ayrı kutuya koyup iki ayrı kişiye yollasın. Bohr'a göre kutuları alanlar içine bakmadıkça kutudaki eldiven hem sağ hem sol özellik gösterir (Gerçekte böyle bir şey yok, eldivenin atom gibi davrandığını düşünün). Kutuyu açıp bakınca karşımızda sol eldiven görüyorsak diğer eldivene bakmamıza gerek yoktur, onun sağ eldiven olduğu açıktır.
Burada ilk eldivenin sol olarak ölçülmesi, diğer eldivenin (o da kutu kapalı iken hem sağ hem sol özelliğin karışımı) "anında" sağ teke dönüşmesini gerektirir. Bu durumda sağ eldiven bir sağ/sol karışımı hâlinde iken eşinin "sol" olarak ölçüldüğünden "anında" bilgisinin olmasını gerektirir. Ne kadar uzakta olurlarsa olsunlar! Einstein bu duruma şiddetle karşı çıkıyordu çünkü bilgi ışık hızından hızlı hareket edemezdi, Bohr ve Heisenberg'in bu saçmalıkları özel görelilik kuramını çiğnemekteydi.
Einstein'e göre zaten biz ölçsekte ölçmesekte sol eldiven sol özellik, sağ eldiven sağ özellik göstermelidir. Çok mantıklı değil mi?
Bir başka itiraz "Kutudaki saat" deneyi ile Heisenberg'in belirsizliğinedir. Einstein dehasını kullanıp Kuantum'u dart tahtası gibi hedefine koymuş, saldırıp duruyordu. Düşünsenize, elinizle büyüttüğünüz bebeğinizi ergenliğe gelince öldürmek istiyorsunuz. İroni...
1930 Solvay Konferansı. İki dev aynı karede. Einstein ve Bohr. Einstein bu konferansta "kutudaki saati" Bohr'un kucağına bırakır...
Einstein bu deneyi konferans esnasında ileri sürünce Bohr'un bütün keyfi kaçtı. O gece hiç uyuyamadı. Çok gergindi. Einstein öyle parlak bir zeka örneği ile bir düşünce deneyi kurgulamıştı ki, anlatmayı bitirince Bohr şaşkın, o zafer edasındaydı.
Ancak Einstein karşısındaki kurdu fena hafife almıştı.. Deneye bir bakalım mı?
Belirsizlik ilkesi (ilke2) enerji ile zaman ölçümlerinin de aynı anda aynı hassasiyetle yapılamayacağını söyler. Einstein bunu çürütmek için şöyle bir deney düzeneği kurgular; Kapalı bir kutunun içine bir saat koyalım. Kutunun içinde bir tane de foton yani ışık taneciği olsun. Kutuda bir kapak var ve bu kapak da saate bağlı olsun. Öyle ki, kapağı açıp kapatınca kutudaki saat bu "belirli" zaman farkını ölçebilsin.
Şimdi diyor Einstein; kapağı açalım ve foton dışarı fırladığı anda kapağı kapatalım. Belirli bir zaman geçti değil mi? Peki enerji? Kapak açılmadan önce yani foton henüz kutuda iken kutunun ağırlığı ölçülür. Kapak açılıp kapandıktan yani foton dışarı çıktıktan sonra kutunun ağırlığı bir daha ölçülür. Kutunun "hafiflemesi" gerekmektedir.
Aradaki fark fotonun kütlesi midir? Kütlesidir... Kütle enerji değil midir? (E=mc2) Enerjidir.. Kaçan fotonun "BELİRLİ" bir kütlesi var mıdır? vardır.. Dolayısıyla BELİRLİ bir enerji değişimi var mıdır? Vardır.. Einstein Bohr'a BAK GÖRDÜN MÜ HEMŞERİM DEMEK Kİ hem zamanı, hem de enerjiyi kesin bir şekilde ölçebiliyormuşuz. Bohr yutkunur, birşey söyleyemez fena halde canı sıkılır, dışarı çıkar...
Bohr'u çok gergin bir akşam yemeği ve uykusuz bir gece bekliyordur. Heisenberg'in, yol arkadaşının belirsizlik ilkesi, kariyeri, bütün çalışmaları, Kuantum kuramı Kopenhag yorumu göz göre göre çöpü boylamak üzereydi. Bir çare bir çare ama nasıl bir çare?
Uzun bir gecenin sonunda güneş doğduğunda Bohr'un yüzü gülüyordu. Belirsizlik ilkesi hâlâ geçerliydi.. Nasıl mı?
Kutudan ayrılan fotonun kütlesi yani enerji değişimi belirli idi buna denilecek söz yoktu. Ancak sıkıntı zaman ölçümünde idi. Foton kutuda iken kutunun momentumu sıfırdır, yani hareketsizdir. Foton kutudan ayrıldıktan sonra kutuyu "geri iter" tıpkı yukarda silahtan ayrılan merminin silahı geri teptirmesi gibi. Yani kutu artık sıfır momentum değil belli bir momentum değerine sahip olur. Bu da kutudaki saatin akış hızını değiştirir. (Özel görelilik kuramı) Dolayısıyla zaman ölçümü belirsizdir.
Bohr, Einstein'i sadece kendi silahıyla (özel görelilik) vursa iyi, üstüne üstlük bir de Einstein'in belirsizliği çürütmek için ortaya attığı deneyin aksine Belirsizlik ilkesini ispatladığını gösterdi :-) İroni!
Einstein bu sözü ne zaman söylemiş tespit edemedim ama eminim ki o bile alışmakta zorlanıyordu Kuantumun bu durdurulamaz yükselişine.
Ancak Kopenhag yorumuna çok geçmeden başka bir devden, hem de yine Einstein gibi Kuantumu besleyip büyüten başka bir devden itiraz geldi Erwin Schrödinger. Kuantum kuramının en büyük emekçilerinden. Ancak onun da Einstein gibi Kopenhag yorumundan midesi bulanmıştı bir kere.
Schrödinger "meğerse koynumuzda yılan beslemişiz" deyip zekice başka bir düşünce deneyi ortaya attı: Kutudaki Kedi...
Bu deneyin nasıl yapıldığı ile ilgili sayısız kaynak var. Ancak "neden" Schrödinger bu deneyi tasarlama gereği duymuş, deney ne ima etmektedir gibi can alıcı yerlerin tartışıldığı pek az yazı olduğunu farkettim. Biz üzerine biraz gevezelik edeceğiz.
Schrödinger, Bohr ve Heisenberg ortak yapımı Kopenhag ilke-1'den çok rahatsız idi.
İlke1: Bir sistem, üzerinde ölçüm yapılana dek bu sistem olası bütün durumları (ihtimallerin) içinde barındıran ya da başka deyişle
Bu yüzden 1935 yılında kaleme aldığı bir makaleyle ilke1'in mantıksızlığını ortaya koymaya çalıştı.
Mantıksızlık, süperpozisyon durumunda bulunan bir sistemin gerçekliğini "gözlem yoluyla" belirmekteydi. Bence de ya. Yürü be Schrödinger :-)
Bunun için yapılması gereken, bu mantıksız durumu mikro dünyadan makro dünyaya yansıtıp bu duruma dikkat çekmekti.
Deney şöyle efendim; canlı bir kedi içinde zehirli bir şişe olan bir kutuya konur. Kutuda ayrıca radyoaktif bir düzenek vardır.
Radyoaktif düzenek içinde 1 saat içinde bozunma ihtimali %50 olan bir atom var. Şayet atom bozunursa çekiç zehir dolu şişeyi patlatır. Şişe patlarsa kedi ölür. Ya da atom bozunmaz, kedi de ölmez. Soru şu, 1 saat sonunda kutunun içindeki kedinin durumu nedir?
Aklı başında herkes şunu söyler; kutuyu açıp bakmak lazım. Bunu düşündüyseniz gerçekten normalsiniz. Bir sıkıntı yok. (İroni değil :-)) )
Şimdi biz önce Kopenhag ilke1 ne diyor ona bakalım. Bu ilke atom için şunu söyler; atom bozunmuş veya bozunmamıştır iki durum üst üste binmiştir. Yani atomik ölçekte bir süperpozisyon durumu var. Kutuyu açarsak bu iki durum bizim gözlediğimiz ve "gerçeklik" dediğimiz duruma "çöker". Madem atomun kaderi ile kedinin kaderi ortak, o halde kedi de süperpozisyonda yani hem canlı hem de ölü olmak zorunda Schrödinger, işte bu mantıksız noktaya dikkat çeker. Gerçekliği gözlem ediminin bir sonucu haline getirme mantıksız der yani.
Bu düşünce deneyi esasen Schrödinger'in ilke-3'ü gözardı etmesinden dolayı yılan hikayesine dönmüştür.
İlke3: Mikro dünya mikro yasalarıyla (Kuantum mekaniği) Makro dünya makro yasalarıyla (Klasik Mekanik) açıklanabilir.
Her ne kadar Kopenhag yorumu ilk başta kedi için hem canlı hem de ölü bir "zombi" hâli öngörse de, Bohr da zaten bunun saçma olduğunun farkındaydı, problem aslında iki dünyanın birbiriyle tutarlı olması gibi. gerekiyormuş gibi yapılan yaklaşımlarımızda!
O yüzden "şansımızı fazla zorlamamıza gerek yoktur". Şansımızı zorlarsak neler oluyor bakalım mı? Bir defa şansımızı zorlamak demek yani illa "ben kediyi ölü veya diri istiyorum" demek Hugh Everett'in çoklu dünyalar yorumuna görülebilir.
Everett kutuyu açtığımız anda kedinin ölü ve canlı olduğu iki evrenin de misafiri oluruz diyor. Yani kediyi ölü gördüysek aslında onun ölü olduğu evreni, canlı gördüysek onun canlı olduğu evreni "birlikte yaratıyoruz". Yani gözlemci ve kediye özel iki evren!
Roger Penrose bu açıklamanın Kuantum mekaniği ruhunu yansıtmadığını ileri sürerek reddetmiştir. Şansımızı biraz daha zorlayalim mı?
Başka bir yoruma göre gözlemci bilinçli bir varlık olmak zorunda değil. Kedi kendi kendisinin gözlemcisi olabilir ve kendi kaderini bize bağlı kalmadan önceden zaten yaşamıştır çünkü dalga fonksiyonunu bizzat kendisi çökertmiştir. Hatta kutunun kendisi bile bir "çevresel gözlemci" sayılabilir ve doğal olarak kutunun dışından ve dış gözlemcilerden bağımsız, kedinin durumu netleşebilir.
Bu açıklamanın çelişkisi ise örneğin kedi gözlemcisi için dalga fonksiyonu çökmüş olabilir; ama kutuya dışardan bakacak biri için hâlâ kedinin süperpozisyon geçerlidir ve bunu iddia etmeye hakkı vardır. E ne oldu şimdi? Error. Yine demek ki şansımızı zorluyoruz.
Kişisel fikrimdir, ben de bu konuda (ve çoğu konuda) Bohr ve Kopenhag ilke3 gibi düşünüyorum. "İki dünyayı karşı karşıya getirmeyin" :-)
Genel bakış açısıyla; Kopenhag yorumunun hem EPR'de ki dolanıklık hem de kedi deneyindeki süperpozisyon paradokslarına sanki biraz "kaçamak" cevaplar verdiğini farketmiş olabilirsiniz. Mesela ilke-3 sanki daha da emredici gibi, "bu böyle sorgulama" der gibi.
Ancak deneysel bulgular ve elde edilen veri istatistikleri, parçacıklar dünyasının gerçekten de "keyfi" ve "rastlantısal" davrandığını desteklemekte, yani Bohr ve Heisenberg duruşunun daha uygun bir yaklaşım olduğunu göstermektedir. Ancak yine de bazılarınız hâlâ itiraz ediyor olabilir, nasıl olurda bizim "gerçek dünya" dediğimiz klasik dünyanın temelleri böylesine fantastik bir kaos dünyasının üzerinde yükselmektedir? Bu derin bir çelişki değil midir? Deyip Einstein'a arka çıkabilirsiniz. Ancak doğa böyle. Buna alışmak zorundayız gibi.
Belki de bu uyuşmazlığın kaçınılmaz oluşu yüzden "iki dünyayı" birlikte açıklayabilecek "Herşeyin Teorisini" bulamıyor olabiliriz.
Feynman bu paradoksun ileride yeni deneyler ve verilerin daha detaylı analizi ile aşılabileceği konusunda ümitlidir.
Richard Feynman. Ona göre Kuantum Mekaniğinin bütün ilkeleri sadece tek bir deneyin anlaşılması ile ortaya konabilirdi: Çift yarık deneyi.
Çift yarık deneyini görsellerle anlatmak hem anlatan hem okuyanlar için zorlayıcı olacaktır. Bu yüzden basit bir videosuna bakalım. Konu sade bir anlatımla ele alınmış. Bizim yapacağımız ise üzerine konuşmak. Buradan yakınız:
Video, "birinin bizi izlediğini fark ettiğimizde davranışlarımız değişir" şeklinde başlıyor. Analojiyi bunun üzerine inşa edelim. Şimdi, Aslı yaramaz ama aynı zamanda çok zeki bir öğrenci. Asım ise onun öğretmeni olsun.
Burada Aslı'nın hem "yaramaz" hem de "zeki" olması ışığın (ya da elektronun) hem dalga hem de tanecik olması gibi düşünülsün. Asım öğretmen ise Aslı'nın okul davranışlarını değerlendirecek rehber öğretmen olsun. Yani deneydeki dedektör ya da "algılayıcı".
Aslı, Asım öğretmen tarafından denetlenmediği müddetçe yaramazlık (dalga) yapacaktır. Tabi zeki olma durumu da (tanecik) kendinde saklı. Ne zaman ki Asım öğretmen sınıfa girer (dedektör ve algılayıcı açılır) o zaman Aslı anında yaramazlığa (dalga) son verip zeki (tanecik) öğrenci rolüne bürünür. Burada kilit nokta ASIM ÖĞRETMEN ASLI'YI NE DEĞERLENDİRMEK İSTESE (ÖLÇÜM) ONU HEP VE SADECE ZEKİ BİR ÖĞRENCİ OLARAK ÖLÇECEKTİR. Asım öğretmene göre "gerçek olan" ölçüm sonucudur ancak "gerçeklik" Aslı'nın aslında sadece zeki olmadığı, aynı zamanda yaramaz olduğudur.Bohr ve Heisenberg şunu savunuyordu;"ölçüm,çok sayıda durum içinden (gerçeklik) sadece birinin (gerçek) dışavurumundan ibarettir". Bu, küçüklerin dünyasında geçerli ve sayısız kez kanıtlanmış bir kuraldır.
Deneye gelince;
Işık veya elektron (hatta atomlar) kaynaktan çıkıp yol alırken dalga biçiminde yayılmakta iken eğer bir şey onları rahatsız ederse (Dedektör açılırsa) tanecik karakteri gösterirler. Bu teknik bir konu olmasına rağmen yine analoji kurarak somutlaştıralım.
Dedektör elektronun hangi yarıktan geçtiğini "görmek" için, ondan sıçrayıp gelecek bir foton (ışık) tespit etmesi gerekir. Burada fotonun elektron ile etkileşim göstereceği açıktır.Bu da elektronun dalga doğasını terkedip tanecik gibi davranmasını gerektirir. Şayet dedektör kapalı olursa, o zaman elektron kaynaktan çıkıp ekrana düştüğü ana dek dalga doğasıyla yayılım gösterecektir. Ne zaman bu dalga ekrana "toslar", işte o zaman ekran ile etkileşim göstereceği için tanecik konseptine döner ve ekranda iz bırakır.
Bakın burada ekrana "tek tek" gönderilen elektronların oluşturduğu girişim desenlerini görüyorsunuz.
İlk etapta (a) anlamsız yerlere düşmüş bu elektronlar farkettiyseniz. Ama giderek daha fazla elektron ekrana düştükçe bir girişim örüntüsü meydana gelmeye başlıyor. Elektronlar tek tek gönderildiği için tek bir yarıktan geçmesi beklenirken tek bir elektron sanki dalga gibi iki yarıktan birden geçiyor ve desen oluşturuyor! Bu nasıl açıklanabilir?
Bunun tek açıklaması elektronun bir dalga karakteri taşıdığı (de Broglie'yi hatırlayalım) ve kendi dalgasının iki yarıktan birden geçip yine kendisiyle girişim yapması sonucu desen oluştuğunu varsaymaktır. Burada dedektör kapalı idi. Dedektör açık olsaydı "Elektron dalgası" dedektör tarafından rahatsız edilecek,dolayısıyla tanecik konseptine dönecek ve ardından "mecburen" tek bir yarıktan geçerek ekranda bir desen yerine sadece iki paralel çizgi oluşacaktı. Çift yarık deneyinin altında yatan budur.
Peki, kurnazlık yapıp elektron "yarıklardan geçtikten sonra" onun dalga mı tanecik mi olduğunu belirlesek? Kurnazlık diyoruz, çünkü elektron yarıklarından ya dalga ya da tanecik olarak geçip bize geldikten sonra biz onu ölçtüğümüzde artık "aaa durun ya ama çok kötüsünüzzz ben hazırlıksız yakalandım durun bi tekrar geri dönüp ona göre geleyim ben" deme şansı olabilir mi?
Tekrar ediyorum son kısmı; çok önemli çünkü. Kurnazlık şurada; bu elektron yarıklardan dalga olarak geçtiyse biz ölçümü o yarıktan geçtikten sonra yaptığımız için onu dalga olarak ölçmemiz gerekir ve ekranda desen oluşması gerekir. Artık geriye dönüp durun ben tanecik olma hakkımı kullanmak istiyorum deme şansı yoktur. İş işten geçmiş olmalıdır. Mantıklı değil mi?
Şimdi derin nefes alın. Ve sakin olmaya çalışın. Yarıklardan geçip ekranda girişim deseni bırakan elektronları (yani yarıklardan dalga olarak geçtiği besbelli) ekrana düşmeden hemen önce (yani çoktan yarıklar geride kalmış) izleyince ekrandaki desen kayboluyor! Ve sadece iki paralel çizgi oluşuyor tekrar! Sanki yarıklardan tanecik olarak geçmiş gibi!
Bu şoku atlatmaniz uzun sürebilir. Elektron bildiğiniz "Demek sen beni faka bastırmaya çalışırsın ha, dur geri dönüp bu kez tanecik olarak geri dönüyorum, seni gidi hain domdom" diyor bize. YAPTIĞIMIZ BİR SEÇİM SADECE GELECEĞİ DEĞİL, GEÇMİŞİ DE DEĞİŞTİRİYOR!
Buna inanmıyorum, bu saçmalık diyenler en son yapılan şu çalışmaya göz atabilirler. Kuantum dünyasında mantığa pek yer yoktur. Peki yine de bir tutam mantık kullanıp açıklamaya çalışsak? Feynman parçacıkların bir A noktasından B noktasına seçili bir yoldan gitmediğini söyler. Dolayısıyla bütün uzaya "yayılmıştır".
Sonsuz sayıda yolu aynı anda kullanır parçacık. Öyle ki, bir yarıktan geçse bile geri dönüp diğer yarıktan da geçebilir :-) (mor yol)
Sizi rahatlatacak bir açıklama yapmayı çok isterdim. Ancak durum maalesef bu. Eğer Kuantum Dünyasında yaşıyor olsaydınız şu anda yaptıklarınız, gelecekte bir başkasının yapacağı seçim tarafından şekillendirilebilirdi. Başka bir deyişle, geçmişiniz, henüz yaşanmamış varsaydığınız geleceğinizi inşa eden değil, onun tarafından inşa edilmiş bir kavram olacaktı.
Bu noktaya dek size Kuantum teorisinin bilimsel bir betimlemesini sunmaya çalıştım. Felsefesi ve çıkarımlarını ise siz değerli dostlara bırakmak istiyorum.
Gerçek ve gerçekliğin en temelde derin bir ayrım içerdiğini düşünen Bohr ile doğayı bir bütün olarak birbiriyle tutarlı ilişkiler içinde ele alma gayretini son nefesine dek sürdüren Einstein' in güzel bir karesi ile bitireceğiz. Niels Bohr, Albert Einstein. Aralık, 1925.
KAYNAK :
Bu yazı, Twitter'da Bohringerstein kullanıcısının oluşturduğu Kuantum Teorisi Zinciri'nin, kendisinden izin alınarak düz yazıya çevrilmesi ile oluşturulmuştur. Benim alıntıladığım yazı, düz yazıya çevirirken yapılması gereken minik düzeltmeler hariç, Twitter zincirinin kopyala-yapıştır versiyonudur.
Yazının sahibi Bohringerstein , düzeltmeler ve eklemeler yaptığı yazının son halini Bilimfili sitesinde yayınladı. O yazıya da aşağıdaki bağlantıdan ulaşabilirsiniz;
https://bilimfili.com/kuantum-teorisine-genel-bir-bakis/
Herkes için Kuantum Teorisi
 Reviewed by Fırat Tarman
on
Mart 22, 2017
Rating:
Reviewed by Fırat Tarman
on
Mart 22, 2017
Rating:
 Reviewed by Fırat Tarman
on
Mart 22, 2017
Rating:
Reviewed by Fırat Tarman
on
Mart 22, 2017
Rating:













































































































Hiç yorum yok: